겉바속촉
[PYTHON] 파이썬_이진검색, 검색시간비교 본문
안녕하세요
겉바속촉입니다
!^^!
!!파이썬 시작하기!!

이번에는 선형검색에 이어
이진 검색에 대해서
알아보도록 하겠습니다.
2021/01/07 - [IT 일기 (상반기)/PYTHON] - [PYTHON] 파이썬_리스트 검색
[PYTHON] 파이썬_리스트 검색
안녕하세요 겉바속촉입니다 !^^! !!파이썬 시작하기!! 리스트 검색에 대해서 알아보도록 하겠습니다 리스트 검색 리스트의 특정 항목을 검색하는 INDEX 메서드 리스트 앞에서부터 차례로 각 항목
2-juhyun-2.tistory.com
이진 검색
선형검색은 데이터가 많아질수록 비례해서 선형으로 증가합니다
그래서 이번에 배우는 이진 검색 binary search!!!
정렬된 리스트를 사용하여 중간값을 비교하며 값을 찾는 검색 방법
그래서 검사하는 데이터가 많아지더라도 서서히 증가하기 때문에 선형검색보다 시간 단축면에서 좋습니다.
이진 검색 코드
우리가 알아야할 것은
리스트의 양 끝단에 i와 j를 두고 중간값인 m을 사용해서
찾는 값과 중간 값을 비교해가면서 검색할 범위를 훅 줄여버리는 것입니다.
큰 쪽의 반 or 작은 쪽의 반
즉 루프를 돌때마다 검색할 범위가 반씩 줄어드는 거에요:)
from typing import Any
# [1, 3, 4, 4, 5, 7, 9, 10]
# i j
# m
def binary_search(lst: list, value: Any) -> int:
i = 0 # 리스트의 시작 인덱스
j = len(lst) - 1 # 리스트의 끝 인덱스
while i != j + 1:
m = (i + j) // 2 # m: i와 j의 중간
if lst[m] < v: # 내가 찾고자 하는 값보다 작다면
i = m + 1 # i는 m 다음 항목으로 옮긴다
else: # 내가 찾고자 하는 값보다 크거나 같다면
j = m - 1 # j는 m 이전 항목으로 옮긴다
if 0 <= i < len(lst) and lst[i] == v: # i가 0이상이고 리스트 범위내에 있고 and 찾고자하는 값과 동일하다면
return i
else:
return -1
얘도 시간이 얼마나 걸리는 지 측정해볼게요
참고로 지난번에 했던 선형검색과 비교해보기 위해 함께 출력했습니다:)
지난 번 포스팅 참고해주세요:)
2021/01/07 - [IT 일기 (상반기)/PYTHON] - [PYTHON] 파이썬_리스트 검색
[PYTHON] 파이썬_리스트 검색
안녕하세요 겉바속촉입니다 !^^! !!파이썬 시작하기!! 리스트 검색에 대해서 알아보도록 하겠습니다 리스트 검색 리스트의 특정 항목을 검색하는 INDEX 메서드 리스트 앞에서부터 차례로 각 항목
2-juhyun-2.tistory.com
def print_times(v: Any, L: list) -> None:
t1 = time.perf_counter()
L.index(v)
t2 = time.perf_counter()
index_time = (t2 - t1) * 1000.0
while_time = time_it(linear_search_while, L, v)
for_time = time_it(linear_search_for, L, v)
sentinel_time = time_it(linear_search_sentinel, L, v)
binary_time = time_it(binary_search, L, v)
print("{0}\t{1:.2f}\t{2:.2f}\t{3:.2f}\t{4:.2f}\t{5:.2f}\t".format(
v, while_time, for_time, sentinel_time, binary_time, index_time))
L = list(range(10000001))
print_times(10, L)
print_times(5000000, L)
print_times(10000000, L)
결과
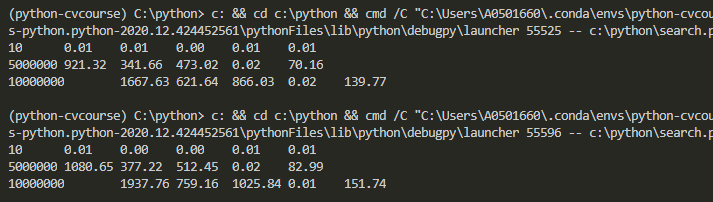
오 역시 binary 검색 방법이 원하는 값을 찾는 데
월등하게 빨리 찾고있네요!!!
선형검색과 이진검색 그리고 시간측정까지 하는 전체코드
from typing import Any
def linear_search_while(lst: list, value: Any) -> int:
'''lst에서 처음으로 나오는 인덱스를 반환하거나 lst에 value가 없는 경우 -1을 반환한다.'''
# 0 1 2 3 4 5
# [1, 2, 3, 4, 5, 6]
# len => 6
i = 0 #lst 내에서 검사할 다음 항목의 인덱스
while i != len(lst) and lst[i] !=value:
i = i + 1
if i == len(lst):
return -1
else:
return i
def linear_search_for(lst: list, value: Any) -> int:
for i in range(len(lst)):
if lst[i] == value:
return i
return -1
def linear_search_sentinel(lst: list, value: Any) -> int:
#센티널을 리스트 마지막에 추가
lst.append(value)
i = 0
while lst[i] != value:
i = i + 1
# 센티널을 제거
lst.pop() #리스트를 원래 상태로 만듦
# 일치하는 값의 위치가 센티널과 동일한 지를 확인
if i == len(lst):
return -1
else:
return i
# lst = [ 2, -3, 5, 9, 8, -6, 4, -15 ]
# value = 5
# index = linear_search(lst, value)
# print(index)
from typing import Any
# [1, 3, 4, 4, 5, 7, 9, 10]
# i j
# m
def binary_search(lst: list, v: Any) -> int:
i = 0 # 리스트의 시작 인덱스
j = len(lst) - 1 # 리스트의 끝 인덱스
while i != j + 1:
m = (i + j) // 2 # m: i와 j의 중간
if lst[m] < v: # 내가 찾고자 하는 값보다 작다면
i = m + 1 # i는 m 다음으로 옮긴다
else: # 내가 찾고자 하는 값보다 크거나 같다면
j = m - 1 # j는 m 전으로 옮긴다
if 0 <= i < len(lst) and lst[i] == v: # i가 0이상이고 리스트 범위내에 있고 and 찾고자하는 값과 동일하다면
return i
else:
return -1
import time
from typing import Callable, Any
def time_it(search: Callable[[list, Any], Any], L: list, v: Any) -> float:
t1 = time.perf_counter()
search(L, v)
t2 = time.perf_counter()
return (t2 - t1) * 1000.0
def print_time(v: Any, L:list) -> None:
t1 = time.perf_counter()
L.index(v)
t2 = time.perf_counter()
index_time = (t2 - t1) * 1000.0
while_time = time_it(linear_search_while, L, v)
for_time = time_it(linear_search_for, L, v)
sentinel_time = time_it(linear_search_sentinel, L, v)
binary_time = time_it(binary_search, L, v)
# print("index_time\t", index_time)
# print("while_time\t", while_time)
# print("for_time\t", for_time)
# print("sentinel_time\t", sentinel_time)
# print("index_time\t", index_time)
print("{0}\t{1:.2f}\t{2:.2f}\t{3:.2f}\t{4:.2f}\t{5:.2f}\t".format(
v, while_time, for_time, sentinel_time, binary_time, index_time))
L = list(range(10000001))
print_time(10, L)
print_time(5000000, L)
print_time(10000000, L)
'IT 일기 (상반기) > PYTHON' 카테고리의 다른 글
| [PYTHON] 파이썬_정렬 알고리즘 (병합정렬) (0) | 2021.01.07 |
|---|---|
| [PYTHON] 파이썬_정렬 (선택정렬, 삽입정렬) (0) | 2021.01.07 |
| [PYTHON] 파이썬_리스트 검색 (0) | 2021.01.07 |
| [PYTHON] 파이썬 _가장 작은 두 값 찾기 (0) | 2021.01.06 |
| [PYTHON] 파이썬_정규식 & re 활용 (0) | 2021.01.06 |




